Preisbildung beim Oligopol

4.2.2.1 Modell von Cournot

Das Cournotsche n-pol

ie Verhaltensannahme im Cournotschen Duopolmodell unterstellt, dass die beiden Oligopolisten "autonom" handeln, d.h. mögliche Reaktionen des jeweiligen Konkurrenten nicht in das eigene Kalkül einbeziehen. Das ist offensichtlich sehr unwahrscheinlich. Dennoch lohnt sich die Analyse. Zum einen handelt es sich um das erste wohlformulierte Oligopolmodell überhaupt, an dem sich die Entwicklung weiterer Modelle wesentlich orientierte, zum anderen kann man das Modell als einen frühen Beitrag zur Spieltheorie begreifen. So handelt es sich z.B. bei der Lösung im weiter unten behandelten Gefangenendilemma um ein Cournot-Gleichgewicht.

Daneben wird angenommen, die Duopolisten konkurrieren, indem sie als Mengenfixierer auftreten. Ihre "Wettbewerbswaffe" ist also die Menge, die sie auf den Markt bringen. Sie konkurrieren nicht über den Preis. Auch das wäre eine plausible Verhaltensannahme, deren Konsequenzen sich selbstverständlich ebenfalls untersuchen lassen (siehe Betrand-Modell).

Obwohl es sich eigentlich um ein statisches Modell handelt, kann man sich den Preisbildungsprozess im Cournotschen Duopol dynamisch vorstellen. Um die Analyse so einfach wie möglich zu gestalten, sei ein Mineralwasserduopol* unterstellt, d.h. es fallen keine Kosten an:

Der Duopolist, der "gerade am Zug ist", maximiert seinen Gewinn (im Mineralwasserduopol: Gewinn = Umsatz), wenn er genau die Hälfte der noch nicht befriedigten Nachfrage anbietet (die direkte Preiselastizität seines Absatzes ist dann eins, was nach der Amoroso-Robinson-Relation seinen Umsatz maximiert). Eine "Spielrunde" soll jeweils einen "Zug" beider Duopolisten umfassen.

Periode 1: Anbieter 1 ist als Monopolist am Markt. Wird die Sättigungsmenge auf $x_S = 1$ normiert, dann ist sein gewinnmaximierendes Angebot $x_1 = 1/2$. Jetzt kommt Anbieter 2 hinzu. Er bietet die Hälfte der noch verbliebenen Nachfrage an: $x_2 = 1/2\cdot(1-x_1)$, also $x_2 = 1/4$ an. Das Angebot beider Duopolisten zusammen beträgt somit $x_1+x_2 = 3/4$.

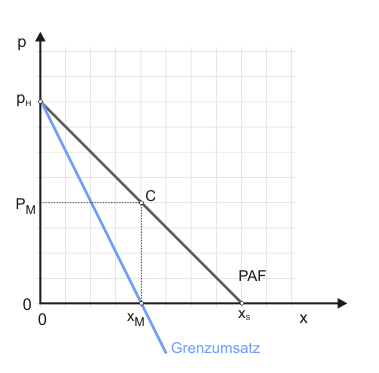
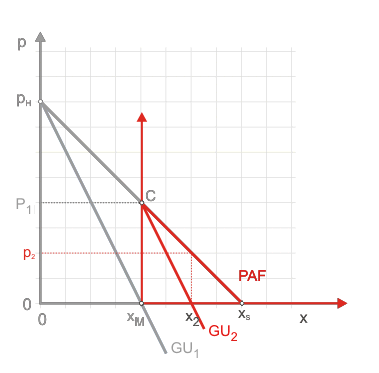
Diese erste Spielrunde ist in der maussensitiven Abbildung 1 dargestellt. Ausgangs ist die Monopolsituation zu erkennen. Wenn Sie das Diagramm anklicken, können Sie die Gewinnmaximierungsüberlegung für Anbieter 2 sehen. Durch sein Hinzutreten sinkt der Preis zum Ende der ersten Runde auf $p_2$.

Periode 2: Anbieter 1 reagiert auf die neue Situation. Er fasst die Angebotsmenge von Anbieter 2 als gegebene Größe auf und geht davon aus, dass Anbieter 2 auf eine Veränderung seines eigenen Angebots nicht reagieren wird. Sein gewinnmaximierendes Angebot ist jetzt $x_1 = 1/2\cdot(1-x_2)$, also $x_1= 1/2\cdot(1-1/4) = 3/8$. Anbieter 2 reagiert aber doch – und zwar in der gleichen Art und Weise wie Anbieter 1 – mit $x_2= 1/2\cdot(1-3/8) = 5/6$. Das gesamte Angebot ist jetzt $11/16$. Und so geht es weiter ... und weiter ... und weiter ...

Periode 3: $\quad{x_1} = {1 \over 2} \cdot \left( {1 - {5 \over 6}} \right) = {{11} \over {32}} \quad\to\quad {x_2} = {1 \over 2} \cdot \left( {1 - {{11} \over {32}}} \right) = {{21} \over {64}} \quad\to\quad {x_1} + {x_2} = {{43} \over {64}}$

Periode 4: $\quad{x_1} = \frac{1}{2} \cdot \left( {1 - \frac{{21}}{{64}}} \right) = \frac{{43}}{{128}} \quad\to\quad {x_2} = \frac{1}{2} \cdot \left( {1 - \frac{{43}}{{128}}} \right) = \frac{{85}}{{256}} \quad\to\quad {x_1} + {x_2} = \frac{{171}}{{256}}$

... oder tabellarisch zusammengefasst:

Wie man Tabelle 1 entnehmen kann. entwickelt sich das Angebot des Anbieters 1 der Reihe ${x_1} = {\left( {\frac{1}{2}} \right)^1} - {\left( {\frac{1}{2}} \right)^3} - {\left( {\frac{1}{2}} \right)^5} - \cdots $ folgend; das Angebot des Anbieters 2 nach ${x_2} = {\left( {\frac{1}{4}} \right)^1} + {\left( {\frac{1}{4}} \right)^2} + {\left( {\frac{1}{4}} \right)^3} + \cdots $.

Um das Angebot von Anbieter 2 nach einer beliebigen Zahl von Perioden berechnen zu können, wird folgende Nebenrechnung vorgenommen:

\[\begin{array}{*{20}{c}} {}&x& = &{{a^1} + {a^2} + {a^3} + ....{a^n}}&{}\\ { - (}&{ax}& = &{{a^2} + {a^3} + {a^4}....{a^{n + 1}}}&)\\ \hline {}&{x - ax}& = &{{a^1} - {a^{n + 1}}}&{}\\ {}&x& = &{\frac{{a - {a^{n + 1}}}}{{1 - a}}}&{} \end{array}\]

Mit dieser Formel bestimmt man für Anbieter 2 mit $a = 1/4$ einen Grenzwert seines Angebots für $n \to \infty $ von $x_2 = 1/3$. Analog kann man für die etwas kompliziertere Reihe von Anbieter 1 die Lösungsformel $x = \frac{{a - 2{a^3} - {a^{n + 2}}}}{{1 - {a^2}}}$ entwickeln und findet für $a = 1/4$ ebenfalls einen Grenzwert in Höhe von $x_1 = 1/3$.

Da beide Anbieter im Gleichgewicht $1/3$ anbieten, spricht man von der Cournotschen 2/3-Lösung.

Um ein Gleichgewicht handelt es sich, da kein Anbieter einen Anlass hat, seine Entscheidung zu ändern, solange der andere bei seiner Entscheidung bleibt. Wenn Anbieter 1 ein Drittel der Sättigungsmenge anbietet, dann ist es für Anbieter 2 optimal, ebenfalls ein Drittel der Sättigungsmenge anzubieten – und umgekehrt.

Man überlegt leicht, dass die Lösung für die beiden Duopolisten bei unverändertem Verhalten zwar stabil, aber nicht optimal ist. Der maximale Umsatz, den der Markt hergibt, ist der Monopolumsatz. Jede andere Menge – wie sie zwischen beiden Anbietern auch immer aufgeteilt sein mag – bringt einen geringeren Umsatz. Die beiden Duopolisten könnten sich also verbessern, wenn sie ihre Produktionsmenge einvernehmlich von $2/3$ auf $1/2$ reduzieren, m.a.W. wenn sie ein Kartell bilden.

Das ist natürlich zugleich ein ganz wesentlicher Kritikpunkt am Cournotschen Oligopolmodell. Die Anbieter werden erkennen, dass sie sich verbessern können. Sie wären also "schön dumm", wenn sie an ihrem stereotypen (autonomen) Verhalten festhielten. Ohnehin werden sie ja von Spielrunde zu Spielrunde enttäuscht, denn entgegen ihrer Erwartung reagiert der Wettbewerber jeweils auf die eigenen Absatzentscheidungen. Der Kritikpunkt stimmt somit überein mit einer Kritik, die auch am Cobweb-Modell geübt wurde: in beiden Modellen sind die Anbieter nicht lernfähig.

Die Mineralwasserannahme stellt keinen Kritikpunkt am Modell dar. Die Hinzunahme von Kosten ändert an den grundsätzlichen Ergebnissen nichts . Und in gewisser Hinsicht besitzt das Cournotsche Gleichgewicht auch Charme, zeigt es doch, dass sich die Duopolisten bewegen müssen, um sich zu verbessern. So kann man vielleicht daraus lernen, dass eine Situation nur vermeintlich optimal ist, weil man versäumt hat, dem Gegner (oder Partner?) Kooperationsangebote zu unterbreiten.

Das wesentliche Ergebnis ist aber folgendes:

Die analoge Verhaltensannahme in einem Tripol-Modell würde eine 3/4-Lösung herbeiführen. Bei vier Anbietern käme es zu einer 4/5-Lösung u.s.w., so dass sich die Angebotsmenge mit der Zahl der Anbieter an die Konkurrenzmenge annähert, die im Mineralwasserfall bei der auf 1 normierten Sättigungsmenge läge. Eine wichtige Botschaft des Cournot-Modells lautet somit, dass mit der Zahl der Anbieter auf einem Markt der Preis sinkt und die Menge steigt. Oder kürzer: